3.8 数字
小数在二进制中不能完全表示
| Ruby | Javascript | Go | Lua | |
|---|---|---|---|---|
| 可变性 | 不可变 | 不可变 | 不可变 | 不可变 |
| 浮点数算术标准 | IEEE754 | IEEE754 | IEEE754 | TODO |
IEEE 754 是一种二进制浮点数算术标准.
1. Ruby
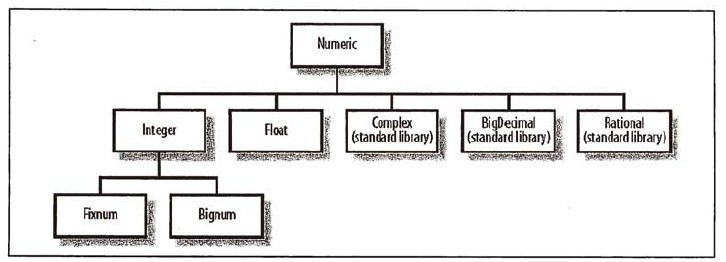
- 所有Ruby数值都是不可变的
- Fixnum最为常用, 因此Ruby将其实现为立即值, 而不是引用
Ruby Float
先看看诡异的浮点数运算:
% irb
>> 0.2*0.2
0.04000000000000001
计算机对小数的表示:
- 固定小数 缺点:不易使用
- 科学计数法
- 单精度: 32位
- 双精度: 64位 1位符号位, 11位指数部, 52位尾数部
限制:
- 计算机中数的表示是有长度限制的
- 计算机中的数是用二进制表示的
总结:
小数不能完全表示
0.2在二进制中是循环小数
浮点数是有限的
- 浮点数是有误差的
- 对于浮点数, 结合法不成立
(a + b) * c误差比a * c + b * c大 浮点数外部(以十进制)表示比较'整', 内部不一定比较'整'
x = 0.0; 10.times {x += 0.1}; x == 1.0 #false有不能比较的时候
两个浮点数比较要求内部表示完全相同才会判定相等
误差会积累
最佳实践:
- 浮点数不能用==比较
- 减少运算次数
对于有精度要求的场景, 使用BigDecimal
require 'bigdecimal' (BigDecimal.new('19.19') * BigDecimal.new('1.234')).to_fBigDecimal做了以下实现:
- 有效的数字自动扩展
- 采用十进制技术
不过天下没有免费的午餐, BigDecimal比Float要慢
2. Javascript
Javascript数字相关的实现只有Number, 不区分整数和浮点数.
NaN
Not a Number, 是一个特殊的number, 表示一个本来要返回number但是没有返回number的情况, 是一种容错的表现形式. 在其他编程语言中, 除零操作将导致异常, 不过javascript中除零会返回NaN, 不会影响代码后续执行.
NaN的特点:
- 一切涉及NaN的操作, 都返回NaN
- NaN与任何值都不等, 包括NaN本身
Javascript提供的函数isNaN, 不是仅仅检测NaN的函数, 而是检测参数是否「不是number」, 也就是通过数值转换也无法变为一个number:
isNaN(NaN) //true
isNaN('red') //true, 无法转换为数字
isNaN(' 9') //false, 可以转换为数字
浮点数问题
Javascript的浮点数算术标准也是基于IEEE 754, 同样也会有表示不精确的现象:
% node
> 0.2*0.2
> 0.04000000000000001
> var x = 0.3 - 0.2 // 0.09999999999999998
> var y = 0.2 - 0.1 // 0.1
> x == y // false
Javascript处理浮点数精度有以下几种选择;
- 存储和操作都转换为整数, 比如钱的存储采用分, 而不是元.
- 使用第三方库, 如sinful.js, mathjs, BigDecimal.js
- 内置函数
toPrecision()toFixed()可以调整浮点数的显示, 不过仅仅是展示.
3. Go
Go 语言中和数字相关的类型有以下这些:
- 整数: int, unit, int16, uint16, int32, uint32, int64, uint64
- 浮点数: float32, float64
- 复数: complex64, complex128
浮点数问题
Go 语言同样存在浮点数精度问题, 稍微不同的是, 浮点数的精度不同, 展示有所不同:
var k float64 = 0.3
var j float64 = 0.2
var i float64 = 0.1
k-j //0.09999999999999998
j-i //0.1
j + i // 0.30000000000000004
k-j == j-i // false
var kk float32 = 0.3
var jj float32 = 0.2
var ii float32 = 0.1
kk-jj // 0.10000001
jj-ii // 0.1
jj + ii // 0.3
kk-jj==jj-ii // false
4. Lua
Number类型代表实数(double-precision floating-point). Lua没有整型,并且也不需要. 有个普遍的误解, 使用浮点型会有算术错误, 一些人害怕浮点型即使一个简单的“加”运算也会有奇奇怪怪的问题。但事实上,用一个double类型来表示一个integer,不存在任何边界问题(除非这个数大于1.0e14). Lua可以表示任何的32-bit的整数,不存在任何边界问题. 除此之外,大多数cpu处理浮点数会比整数要快.
浮点数:
> print(0.2*0.2)
0.04
> print(0.2-0.1)
0.1
> print(0.3-0.2)
0.1
不过还是可以看出浮点数的不精确:
>print(0.3-0.2 == 0.2-0.1)
false